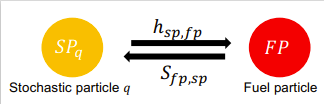Forschungsziele
Die Forschung der Professur Simulation reaktiver Thermo-Fluid Systeme beschäftigt sich mit der numerischen Modellierung reagierender und zumeist turbulenter Strömungen aus gasförmigen, flüssigen und festen Energieträgern. Der Inhaber der Professur ist Prof. Dr. Oliver T. Stein. Die wesentlichen Ziele unserer Forschung sind (i) die Verbesserung unseres grundlegenden Verständnisses von komplexen reagierenden Mehrphasenströmungen, (ii) die Entwicklung prädiktiver Simulationsmodelle für derartige Systeme und damit (iii) ein Beitrag zum weltweiten Übergang hin zu einer nachhaltigen Energiewirtschaft. Wir forschen in enger Zusammenarbeit mit unseren experimentellen Kollegen am Engler-Bunte-Institut und externen Projektpartnern. Wir erreichen unsere Forschungsziele durch die Anwendung und Weiterentwicklung von einer Reihe an Modellierungs- und Analysewerkzeugen, wie im Folgenden dargestellt.
Forschungsthemen
- Direkte Numerische Simulation (DNS) turbulenter reaktiver Strömungen: DNS löst alle Skalen der turbulenten Strömung auf, wodurch hochgenaue Vorhersagen von Strömungen mit niedrigen bis mittleren Turbulenzgraden für grundlegende Untersuchungen ermöglicht werden.
- Grobstruktursimulation (Large Eddy Simulation, LES) turbulenter Strömungen mit chemischer Reaktion: LES löst die größten turbulenten Skalen auf, während kleinskalige Prozesse modelliert werden, so dass genaue Vorhersagen von Strömungen mit mittleren bis hohen Turbulenzgraden in der Forschung und Anwendung erzielt werden können.
- Entwicklung fortgeschrittener LES-Modelle für reagierende Mehrphasenströmungen (flüssige Tröpfchen und feste Partikel): In der LES von Mehrphasenströmungen müssen die Phasenübergänge i.d.R. modelliert werden, um verlässliche Simulationen zu ermöglichen.
- LES-Modellierung mittels der dünnbesetzten Lagrange’schen Multiple-Mapping Conditioning (MMC) Methode: MMC ist ein komplexes aber gleichzeitig hocheffizientes Schließungsmodell für die LES von ein- und mehrphasigen Strömungssystemen.
- LES-Ansätze für die Modellierung von Partikelsystemen mittels der Populationsbilanzgleichung (Population Balance Equation, PBE): Interaktionsprozesse wie z.B. Nukleation, Kondensation, Koagulation, Agglomeration u.a. in Partikel- und Tropfenensembles benötigen fortgeschrittene LES-Schließungsmodelle.
- Machine Learning Ansätze für turbulente reagierende Strömungen: Moderne Machine und Deep Learning Ansätze ermöglichen die effiziente Modellierung komplexer Systeme, Mustererkennung und Featureanalyse.
Forschungsprojekte
|
|
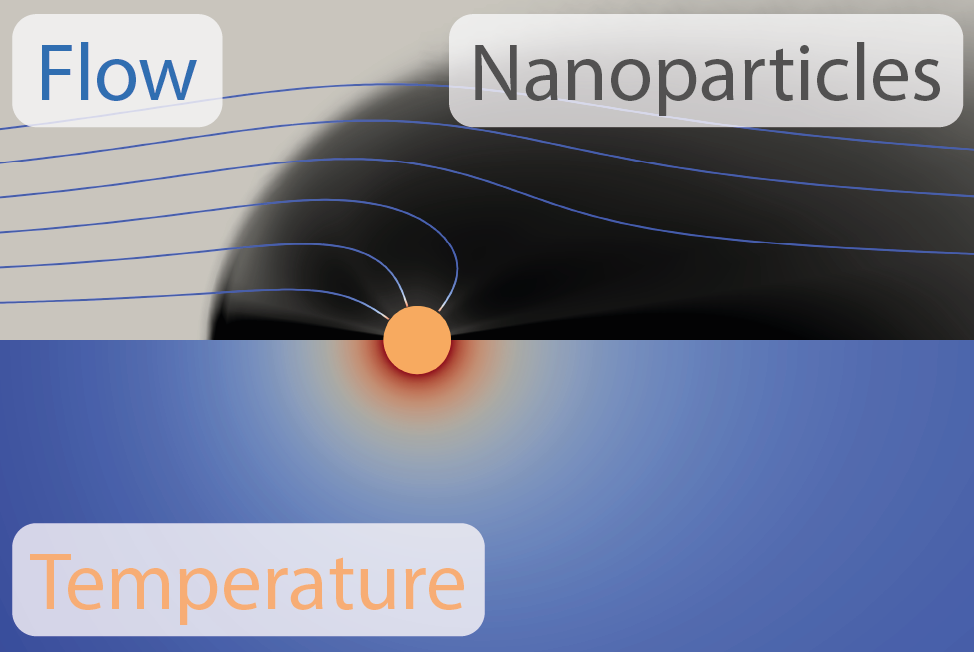
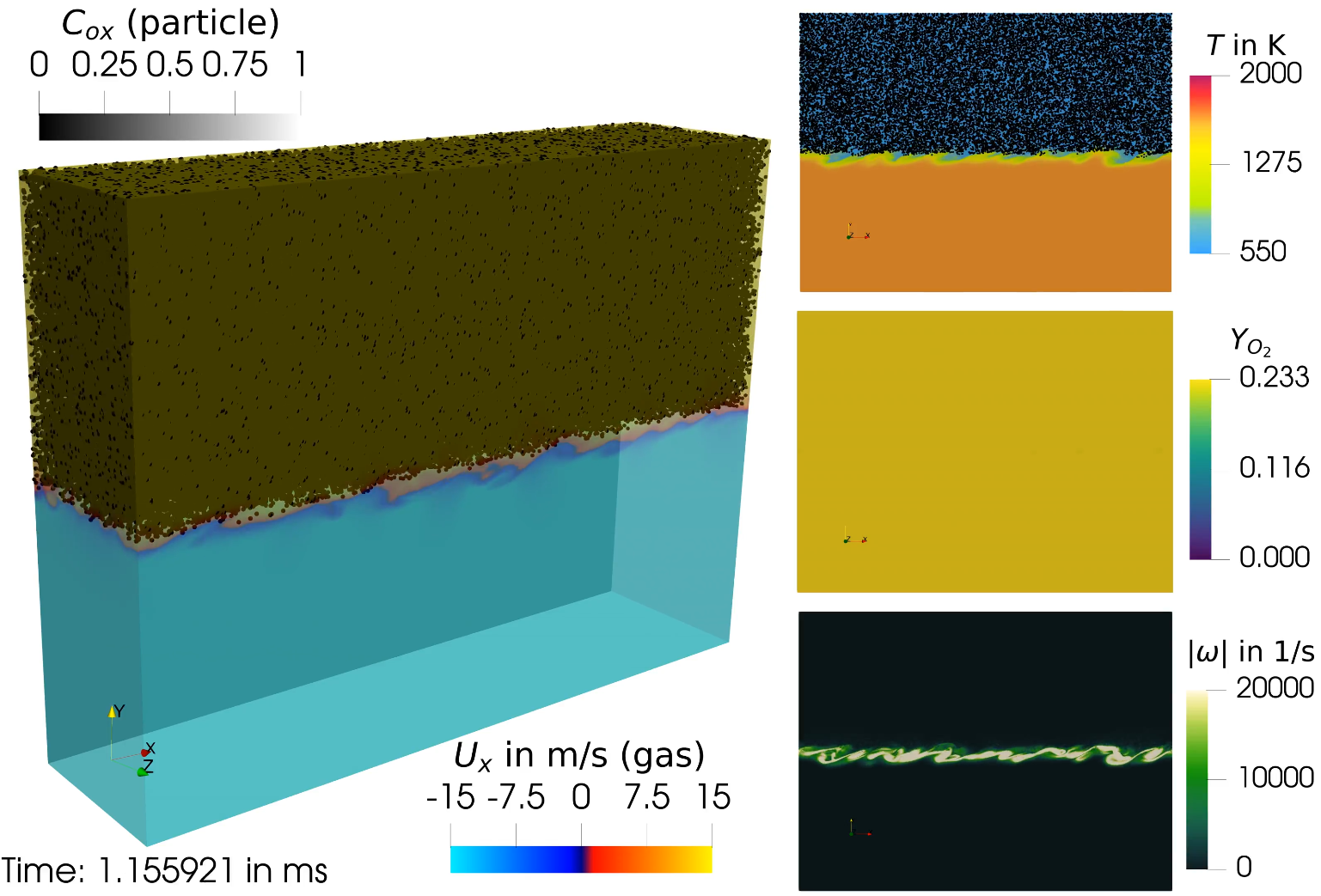
Untersuchung der Nanopartikelabscheidung in der Eisenmikropartikelverbrennung Die Nutzung von Eisenpulver als Energieträger ermöglicht den kostengünstigen, globalen Transport erneuerbarer Energien. Während der Energiefreisetzung mittels Eisenverbrennung können eisenhaltige Nanopartikel entstehen, deren Bildung, Transport und Abscheidung in diesem Projekt simulativ untersucht werden.
https://vbt.ebi.kit.edu/1215.php
|
|
|
Clean Circles - Eisen als Energieträger einer klimaneutralen Kreislaufwirtschaft Eisen als reaktives Metall hat enormes Potential für die Energiewende. Im Projekt Clean Circles erforschen wir fächerübergreifend, wie das Metall zusammen mit seinen Oxiden in einem Kreislauf als kohlenstofffreier chemischer Energieträger genutzt werden kann, um Wind- und Sonnenenergie zu speichern.
Hauptprojekt: https://www.tu-darmstadt.de/clean-circles/about_cc/index.de.jsp
Teilprojekt am EBI-TFS: https://vbt.ebi.kit.edu/1074.php |
|
|
Das DFG-Schwerpunktprogramm SPP 2419 HyCAM (Hydrogen-based fuel combustion using additive manufacturing) befasst sich mit der Optimierung thermochemischer Energiewandlungsprozesse zur flexiblen Nutzung wasserstoffbasierter erneuerbarer Brennstoffe durch additive Fertigungsverfahren. Das gemeinsame Teilprojekt des KIT und der TU Freiberg untersucht die nicht vorgemischte Verbrennung von Ammoniak in maßgeschneiderten porösen inerten Medien.
Hauptprojekt: https://spp2419.itv.rwth-aachen.de/
Projektträger: |
|
|
Dünnbesetzte Partikel-Methoden für die Feststoffverbrennung |
|
|
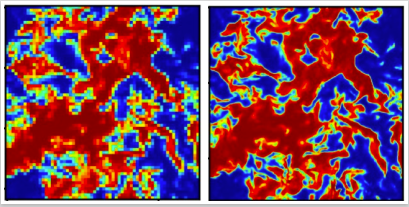
Deep Learning für die verbesserte Simulation der Biomassestaubverbrennung |
|
|
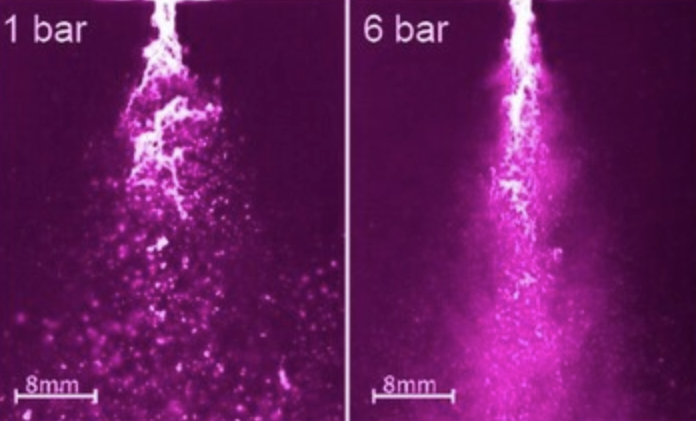
Die Zerstäubung ist Kernbestandteil des Vergasungsprozesses, der eine Schlüsseltechnologie für die kohlenstoffneutrale Bereitstellung von Chemikalien und Energie darstellt. Im Rahmen des MTET-Programms erforschen wir detaillierte Rechenmodelle für die Zerstäubung von hochviskosen Flüssigkeiten im Sinne eines Virtual Spray Test Rig.
Hauptprojekt:
Teilprojekt:
|